Math Concept Points – Grade 8

ALGEBRAIC EXPRESSIONS, IDENTITIES AND FACTORISATION  

Algebraic Expression    

 

• Terms are formed by the product of variables and constants, e.g.

–3xy, 2xyz, 5x², etc.

• Terms are added to form expressions, e.g. –2xy + 5x².
  • Expressions that contain exactly one, two and three terms  are called monomials, binomials and trinomials, respectively.
  • In general, any expression containing one or more terms with non- zero coefficients (and with variables having non-negative exponents) is called a polynomial.
  • Like terms are formed from the same variables and the powers of these variables are also the same. But coefficients of like terms need not be the same.
  • There are number of situations like finding the area of rectangle, triangle, etc. in which we need to multiply algebraic expressions.
  • Multiplication of two algebraic expressions is again an algebraic expression.
  • A monomial multiplied by a monomial always gives a monomial.
  • While multiplying a polynomial by a monomial, we multiply every term in the polynomial by the monomial using the distributive law a ( b + c) = ab + ac.
    • In the multiplication of a polynomial by a binomial (or trinomial), we multiply term by term, i.e. every term of the polynomial is multiplied by every term in the binomial (or trinomial) using the distributive property.
    • An identity is an equality, which is true for all values of its variables in the equality, i.e. an identity is a universal truth.
    •   An equation is true only for certain values of its variables.
    • Some standard identities:
      • (a + b)² = a² + 2ab + b²
      • (a – b)2 = a2 – 2ab + b2
      • (a + b) (a – b) = a2 – b2
      • (x + a) (x + b) = x2 + (a + b) x + ab

Factorisation

• Representation of an algebraic expression as the product of two or more expressions is called factorisation. Each such expression is called a factor of the given algebraic expression.When we factorise an expression, we write it as a product of its factors. These factors may be numbers, algebraic (or literal) variables or algebraic expressions.

• An irreducible factor is a factor which cannot be expressed further as a product of factors. Such a factorisation is called an irreducible factorisation or complete factorisation.A factor which occurs in each term is called the common factor.The factorisation done by using the distributive law (property) is called the common factor method of factorisation.

• Sometimes, many of the expressions to be factorised are of the form or can be put in the form: a² + 2ab + b², a² – 2ab + b², a² – b² or x² + (a + b) x + ab. These expressions can be easily factorised using identities:

a² + 2ab + b² = (a + b)² a² – 2ab + b² = (a – b)² a² – b² = (a + b) (a – b)

x² + (a + b) x + ab = (x + a) (x + b)

• In the division of a polynomial by a monomial, we carry out the division by dividing each term of the polynomial by the monomial.
  • In the division of a polynomial by a polynomial, we factorise both the polynomials and cancel their common factors.

LINEAR EQUATION IN ONE VARIABLE   

• An algebraic equation is an equality involving variables. It has an equality sign. The expression on the left of the equality sign is the Left Hand Side (LHS) and the expression on the right of the equality sign is the Right Hand Side (RHS).
• In an equation the values of the expressions on the LHS and RHS are equal for certain values of the variables. These values are the solutions of the equation.
• Equations where the expressions which form the equation contain only one variable and the highest power of the variable appearing in the equation is 1, are called linear equations in one variable.
• A linear equation may have linear expressions on both sides of the equality sign.
• To find the solution of an equation we perform the same mathematical operations on both sides of the equation, so that the balance between the LHS and RHS is not disturbed.
• A linear equation may have any rational number as its solution.
• In an equation, variables can be transposed from one side of the equation to the other.

COMPARING QUANTITIES 

• Discount is a reduction given on marked price.

Discount = Marked Price – Sale Price (S.P.)

• Discount can be calculated when discount percentage is given.

Discount = Discount % of Marked Price

• Additional expenses made after buying an article are included in the cost price and are known as overhead expenses.

cost price = buying price + overhead expenses

• Sales Tax is charged on the sale of an item by the government and is added to the Bill Amount.

Sales tax = Tax% of sale amount

• These days, however, the selling prices (known as MRP) include the tax known as VAT (Value Added Tax).

The interest compounded annually is the interest calculated on the previous year’s amount A,

(A = P + I).

• The time period after which the interest is added each time to form a new principal is called the conversion period.
• When the interest is compounded half yearly, there are two conversion periods in a year of duration 6 months each.
• Amount when interest is compounded annually is
•  

where P is Principal

R is Rate of interest

n is Time Period

• Amount when interest is compounded half yearly is

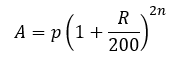
       Where R/100  is half yearly rate and 2n is number of half years.

Mensuration  Concept  Points

• Length of boundary of a simple closed figure is known as perimeter.
• Area is the measure of region enclosed in a simple closed curve.
• Perimeter of a rectangle = 2 (length + breadth).
• Area of a rectangle = length × breadth.
• Perimeter of a square = 4 × side.
• Area of a square = side × side.
• Area of Triangle= ½ Base× Corresponding Height.
• Area of a parallelogram = Base × Corresponding Height.

• Area of a circle =πr ² , where r is the radius.
• Area of a trapezium = ½ × (Sum of parallel sides) × Height.
• Area of a rhombus = 2 × Product of diagonals.
• Lateral surface area of a cube = 4 (side)².
• Total surface area of a cube = 6 (side)².
• Lateral surface area of a cuboid = 2 × height × (length + breadth).
• Total surface area of a cuboid = 2(lb + bh + hl).
• Lateral (curved) surface area of a cylinder = 2rh.
• Total surface area of a cylinder = 2r (r + h), where r is the radius and h is the height.
  • Amount of space occupied by a solid is called its volume.
  • Volume of a cube = (side)³.
  • Volume of a cuboid = length × breadth × height.
  • Volume of a cylinder = r²h.
  • 1cm³ = 1ml
  • 1L = 1000 cm³.
  • 1m3 = 10,00,000 cm3 = 1,000 L.

DIRECT AND INVERSE PROPORTIONS  CONCEPT  POINTS

• Two quantities x and y are said to be in direct proportion if they increase or decrease together in such a manner that the ratio of their corresponding values remain constant.  That is, x/y = = k where
• k is a positive number if x and y are in direct proportion or vary directly. In case of direct proportion, if y1, y2 are the values of y corresponding to the values x1, x2 of x respectively, then

 

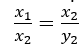
• Two quantities x and y are said to be in inverse proportion if  an increase in x causes a proportional decrease in y and vice-versa, in such a manner that the product of their corresponding values remains constant. That is, xy = k where k is a positive number, if x and y are in inverse proportion. In this case, if y1, y2 are the values of y corresponding to the values x1, x2 of x respectively, then x1 y1=x2y2,   

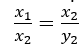
• Quantities increasing or decreasing together need not always be in direct proportion, same in the case of inverse proportion.
• When two quantities x and y are in direct proportion (or vary directly), they are written as x ∞ y. Symbol “∞” stands for ‘is proportional to’.

• When two quantities x and y are in inverse proportion (or vary inversely) they are written as x ∞ 1/y

 

The concept  points  listed  above  is  good  for  quick  update  on revision  of key points. If   you need  tips  of how  to study  mathematics  refer  my  post for the same.